

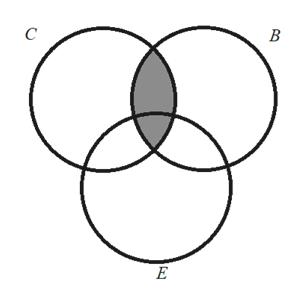
Write a set which contains all the members of your household (and nothing else). When we have two or more sets, we can look at how they are the same or how they differ in lots of different ways.įor example, if set A completely fits into set B, we can say that A ⊂ B. The number of elements in a set: partitions and an example. This contains everything we are interested in and has the symbol '∪', ∪ or \(\upvarepsilon\) (sometimes other symbols are used too). This set could also be defined by us saying:įinally, there is one more important set – the universal set. This is read as 'Z is a set of the factors of 18'. The Venn diagram shows sets 4, B, C, and the universal set U. The usual depiction makes use of a rectangle as the universal set and circles for the sets under consideration.
Shading venn diagrams with 3 sets free#
We can also use notation to create our sets: Shading a Venn diagram with 3 sets: Unions, intersections, all. Views:737191 Instant Access to Free Material What is a Venn Diagram Venn diagram, also known as Euler-Venn diagram is a simple representation of sets by diagrams. Comprehensive Practice Worksheets O' Level and Discrete Mathematics on topic:1. We can define our own sets and choose any letter we want to represent them:


N is the set of counting or natural numbers: Create Venn diagrams to illustrate A B, A B, and A. Basic Venn diagrams can illustrate the interaction of two or three sets. Overlapping areas indicate elements common to both sets. Sets are named using capital letters with some sets having a predefined name. Create Venn Diagrams for Three Sets Online. A Venn diagram represents each set by a circle, usually drawn inside of a containing box representing the universal set. Objects placed within the brackets are called the elements of a set, and do not have to be in any specific order. GCSE IGCSE Maths Mathematics - Venn diagrams - shading regions - identifying regions - differentiated practice worksheets with space for answers - solutions included. Finally, check your answer by moving your mouse pointer over the blank Venn diagram: the answer will appear. Then shade in the parts of this diagram which correspond to the named set. 1 of 10 The whole rectangle contains all the elements being. Describe each region of the Venn diagram using set notation. Set notation uses curly brackets which are sometimes referred to as braces. On a separate piece of paper, re-create the blank Venn diagram shown in the problem. A Venn diagram can show data sets such as preferences in market research. Set notation is used in mathematics to essentially list numbers, objects or outcomes. A c B contains elements outside of A and also in B. A B contains all elements in either set - elements in A or B (or both). So the union of A and B is a bigger set that contains both A and B as subsets.įormally we can write: A∪B =. Example 1 Create Venn diagrams to illustrate A B, A B, and A c B A B contains all elements in both sets - elements in A and B. To denote the UNION of A and B we write: A∪B. It can be used to illustrate the relationships between three sets of data and consists of overlapping circles. We shade all regions that are in either of the sets. We shade the regions the sets have in common. We find a UNION of two sets by taking every element that is in either set and putting all of these elements together into one big set. SHADING VENN DIAGRAMS Recall: M n N is the intersection Of the sets M and N.The Venn diagram shows sets A, B, C, and the universal set U. Finding the Union of Two Sets: Definition of Union: Question: SETS Shading a Venn diagram with 3 sets: Unions, intersections, and C. We may want to have a formal way to "put two sets together" or to "find all the elements that two sets have in common." This desire to find a way to make a new set from one or more old sets motivates us to come up with operations on sets. Z number of elements that belong to set A and B both (A B) W number of elements that belong to none of the sets A or B. Y number of elements that belong to set B only. Sometimes we may want to use one or more sets to create a new set in an interesting way. n ( A B) n (A ) + n ( B ) n ( A B) Where X number of elements that belong to set A only.


 0 kommentar(er)
0 kommentar(er)
